Ancient Egyptian Astronomy & Calendars

Within ancient Egyptian astronomy, there exist complex mythological stories suggesting that in a far distant era, the Earth possessed an ideal 360 day year. And that also the Moon possessed an exacting 30 day Synodic month. Such cosmic harmony was however broken at some point, leading to a great reconfiguration. As a result, the orbital periods of both celestial bodies were transformed to their present values (below). Concerning the Earth year specifically, the ancient Egyptians developed a mythological tale to account for an increase of five extra days: each new day being the birth of a new god (Osiris, Isis, Seth, Nephthys, Horus the Elder).

Myth aside however, in terms of strict astronomical observations, the ancient Egyptians were not so simple as to miss the fact, that the Earth year was far closer to 365.25 days, than 365 days.

Now what is intriguing about ancient Egyptian astronomy is that they wilfully 'embedded' the ideal period of 360 days per year into the actual observed year of just under 365.25 days. The first 360 days were thought to constitute the 'true year'. The additional time that followed of about 5.25 days was held to be 'outside' of the real Earth year, being referred to as 'The Days Upon the Year'.

Indeed, this extra time period was considered to be a dangerous time, as it was also referred to by the ancient Egyptians as 'The Days of the Demons'.

Great Earth Changes Governed By Celestial Laws

In order to prove the Earth once had 360 days per year at a time when the Moon simultaneously had a 30 day month, something very special is required.

The principle or law would have to be mathematical in its expression. And one would expect it also to be simple and elegant.

Now such a principle does indeed exist, and it is very much in line with a certain well accepted astronomical law today: The Harmonic Law of Johannes Kepler.

The Great Discovery of Johannes Kepler

During his lifetime Johannes Kepler (1571 - 1630 AD) discovered a simple mathematical connection between the time taken for a planet to orbit the Sun (Orbital Period) and the mean distance of the planet from the Sun (known as the Semi-Major Axis).

1) The Orbital Period of a body is the time taken to complete a full 360 degree sweep about the Sun.

2) The Semi-Major Axis (SMA) is a planet's average distance from the sun, based upon one complete orbit. Such a component exists because planets do not have perfectly circular orbits, but take an elliptical path about the Sun - an ellipse being a slightly swashed circle. Consequently, all planets have a point of closest approach to the Sun (known as the Perihelion), and a point of furthest approach (known as the Aphelion).

The Mean Distance (SMA) is simply the Perihelion + Aphelion, divided by 2.

Kepler's Law in Action

A precise written statement of Kepler's Law is as follows:

Any change to the Orbital Period (OP) of a planet, squared, is proportional to a change to the Semi-Major Axis (SMA) of the planet, cubed.

Mathematically, Kepler's law is expressed as a basic equation in the following form:

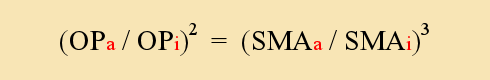
NB: The values with the letter 'i' in red next to them indicate the 'initial' values of a planet. The letter 'a' indicates the 'alternate' values i.e. the new values of a planet's orbit, after some transformation.

Now to understand Kepler's Law we might consider changing the Earth's orbit by way of example.

Using the equation, we start out by substituting in the known (initial) values for the Earth - the current orbital period and the mean distance of the Earth from the Sun, as they exist today:

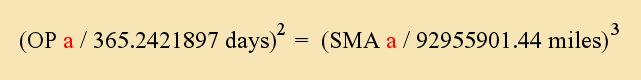
Now with this done, let us suppose I wanted to increase the orbital period of the Earth to 500 days (an alternate value). I would simply place this value in the OPa field:

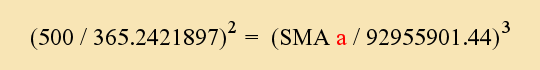
The equation now has only one unknown value: The alternate SMAa value. Mathematically it can be re-arranged to isolate it, and obtain its value:

The answer here given as 114604853.7 miles is the mean distance that the Earth would have to possess were its orbital period altered to 500 days. It would have to increase to this new Semi-Major Axis distance.

The Planet Mars Offers Confirmation

Although a shift to 500 days for the Earth orbit is somewhat abstract, one may consider a very real example that confirms the law in an unmistakable way.

If instead of inputting the value 500, we had inputted 686.93 days, which is the actual orbital period of the planet Mars at this moment, then the SMAa value obtained would be: 141633068.4 miles. This very answer is the observed mean distance (SMA) of Mars right now, accompanying its 686.93 day orbit.

The Law is unbreakable.

If we start out with an orbital period and mean distance for a given celestial body, and specify just one alternate value for either of these variables, it absolutely determines what the other one MUST BE.

A Basic Extension of Kepler's Law Proves An Ideal Earth-Moon System

That the Earth orbit was once 360 days per year at a time when the lunar month was  precisely 30 days, can be proven due to a simple extension of Kepler's law, thus validating ancient Egyptian astronomy.

Just as Kepler was able to demonstrate that a change to the Earth's orbital period is linked to a change to its (own) semi-major axis, there is another law of exactly the same format, further linking the Earth's orbital period directly to the Moon's orbital period i.e. Synodic Month.  

Now in this instance the extended law uses a different combination of powers. Rather than 2 and 3, the powers that govern are 11 and 12. Expressed mathematically though it is very similar to Kepler's Law. Given in equation form, the Earth orbital period here is designated simply TY - Tropical Year:

As before, we can evaluate a change to the Earth-Moon system by starting out with the known present day values for the Earth year and Moon Synodic month. Input into the equation we have the following:

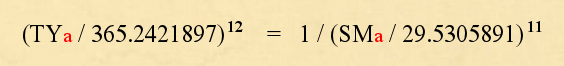
At this point all that needs to be done is to specify one of the unknown variables. In this case the Earth year. The value is set at 360 days - the ideal standard:

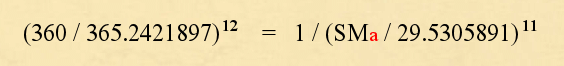
Now just as with Kepler's Law, there is one unknown variable that remains: The Moon Synodic Month (SMa). The equation can therefore be re-arranged to isolate the Synodic month, TO DETERMINE EXACTLY WHAT IT MUST HAVE BEEN WHEN THE EARTH POSSESSED A 360 DAY YEAR:

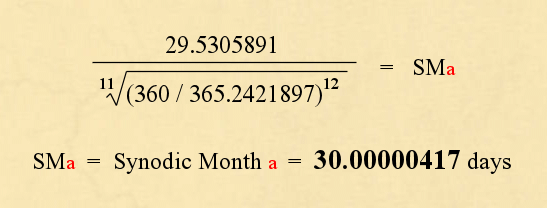
To an exceptional level of precision it is clearly confirmed that when the Earth had a 360 day year the Moon simultaneously had a 30 day month. Now the relationship as described is an inverse one. When the Earth suffers an increase in its orbital period, the moon suffers a decrease in its own.

Now it is important to stress that the mathematical equation here is no mere artificial equation. It captures a true governing principle. The Earth and Moon are bound by this law and physically operate in accordance with it. A real change to the Earth tropical year will cause a real change to the Moon month in line with the mathematics of this equation.

In the face of this Law, the mythological stories behind ancient Egyptian astronomy that spoke of a once ideal Earth-Moon system, are validated.

Next: Sacred Geometry: The Ideal Earth & Imperial Measures

---

Note

[1] The Astronomical Almanac 2003.
Nautical Almanac Office, United States Naval Observatory, and H. M. Nautical Almanac Office, Rutherford Appleton Laboratory. (2001)
Page D2: 29.5305891 Synodic Moon Month

Explanatory Supplement to the Astronomical Almanac.
University Science Books. (1992)
Page 701: 365.2421897 Earth Tropical Year

---

Lost Age Secrets Home